#22. Operations on word vectors
* Cosine similarity
- 두 단어가 얼마나 similar한 지 계산하기 위해 cosine sililarity를 사용한다.
- 두 단어 벡터에 대해:


# GRADED FUNCTION: cosine_similarity
def cosine_similarity(u, v):
"""
Cosine similarity reflects the degree of similariy between u and v
Arguments:
u -- a word vector of shape (n,)
v -- a word vector of shape (n,)
Returns:
cosine_similarity -- the cosine similarity between u and v defined by the formula above.
"""
distance = 0.0
# Compute the dot product between u and v (≈1 line)
dot = np.dot(u, v)
# Compute the L2 norm of u (≈1 line)
norm_u = np.sqrt(np.sum(np.square(u)))
# Compute the L2 norm of v (≈1 line)
norm_v = np.sqrt(np.sum(np.square(v)))
# Compute the cosine similarity defined by formula (1) (≈1 line)
cosine_similarity = dot / (norm_u * norm_v)
return cosine_similarity
* Word analogy task
- "A is to B as C is to _"에서 _가 무엇인지를 구해야 한다.
- ea, eb, ec, ed -> eb - ea ≈ ed - ec와 같은 관계를 가지게 됨.
# GRADED FUNCTION: complete_analogy
def complete_analogy(word_a, word_b, word_c, word_to_vec_map):
"""
Performs the word analogy task as explained above: a is to b as c is to ____.
Arguments:
word_a -- a word, string
word_b -- a word, string
word_c -- a word, string
word_to_vec_map -- dictionary that maps words to their corresponding vectors.
Returns:
best_word -- the word such that v_b - v_a is close to v_best_word - v_c, as measured by cosine similarity
"""
# convert words to lower case
word_a, word_b, word_c = word_a.lower(), word_b.lower(), word_c.lower()
# Get the word embeddings e_a, e_b and e_c (≈1-3 lines)
e_a, e_b, e_c = word_to_vec_map[word_a], word_to_vec_map[word_b], word_to_vec_map[word_c]
words = word_to_vec_map.keys()
max_cosine_sim = -100 # Initialize max_cosine_sim to a large negative number
best_word = None # Initialize best_word with None, it will help keep track of the word to output
# loop over the whole word vector set
for w in words:
# to avoid best_word being one of the input words, pass on them.
if w in [word_a, word_b, word_c] :
continue
# Compute cosine similarity between the vector (e_b - e_a) and the vector ((w's vector representation) - e_c) (≈1 line)
cosine_sim = cosine_similarity(np.subtract(e_b, e_a), np.subtract(word_to_vec_map[w], e_c))
# If the cosine_sim is more than the max_cosine_sim seen so far,
# then: set the new max_cosine_sim to the current cosine_sim and the best_word to the current word (≈3 lines)
if cosine_sim > max_cosine_sim:
max_cosine_sim = cosine_sim
best_word = w
return best_word
* Debiasing word vectors
- word embedding에 gender biases가 포함되어 있는 경우들이 존재하기 때문에 이러한 biases를 제거해주는 작업이 필요하다.
- g = e(woman) - e(man)이라고 하자. 그러면 벡터 g는 gender에 대한 인코딩일 것이다.
- g를 이용해 단어들간의 similarity를 계산해보면:
print('Other words and their similarities:')
word_list = ['lipstick', 'guns', 'science', 'arts', 'literature', 'warrior','doctor', 'tree', 'receptionist',
'technology', 'fashion', 'teacher', 'engineer', 'pilot', 'computer', 'singer']
for w in word_list:
print (w, cosine_similarity(word_to_vec_map[w], g))Other words and their similarities:
lipstick 0.276919162564
guns -0.18884855679
science -0.0608290654093
arts 0.00818931238588
literature 0.0647250443346
warrior -0.209201646411
doctor 0.118952894109
tree -0.0708939917548
receptionist 0.330779417506
technology -0.131937324476
fashion 0.0356389462577
teacher 0.179209234318
engineer -0.0803928049452
pilot 0.00107644989919
computer -0.103303588739
singer 0.185005181365이런 식으로 gender stereotype을 담은 결과값들이 나온다.
- 이러한 bias를 제거해 주는 알고리즘을 사용해보자!
(1) Neutralize bias for non-gender specific words
- 50차원의 word embedding을 사용하고 있다고 하면 space는 다음과 같이 나눠지게 될 것이다.: the bias-direction g와 나머지 49 dimensions(g⊥)

- input embedding e에 대해 e^debiased를 구하는 식은 다음과 같다:

def neutralize(word, g, word_to_vec_map):
"""
Removes the bias of "word" by projecting it on the space orthogonal to the bias axis.
This function ensures that gender neutral words are zero in the gender subspace.
Arguments:
word -- string indicating the word to debias
g -- numpy-array of shape (50,), corresponding to the bias axis (such as gender)
word_to_vec_map -- dictionary mapping words to their corresponding vectors.
Returns:
e_debiased -- neutralized word vector representation of the input "word"
"""
### START CODE HERE ###
# Select word vector representation of "word". Use word_to_vec_map. (≈ 1 line)
e = word_to_vec_map[word]
# Compute e_biascomponent using the formula give above. (≈ 1 line)
e_biascomponent = (np.dot(e, g) / (np.sum(np.square(g)))) * g
# Neutralize e by substracting e_biascomponent from it
# e_debiased should be equal to its orthogonal projection. (≈ 1 line)
e_debiased = e - e_biascomponent
### END CODE HERE ###
return e_debiased
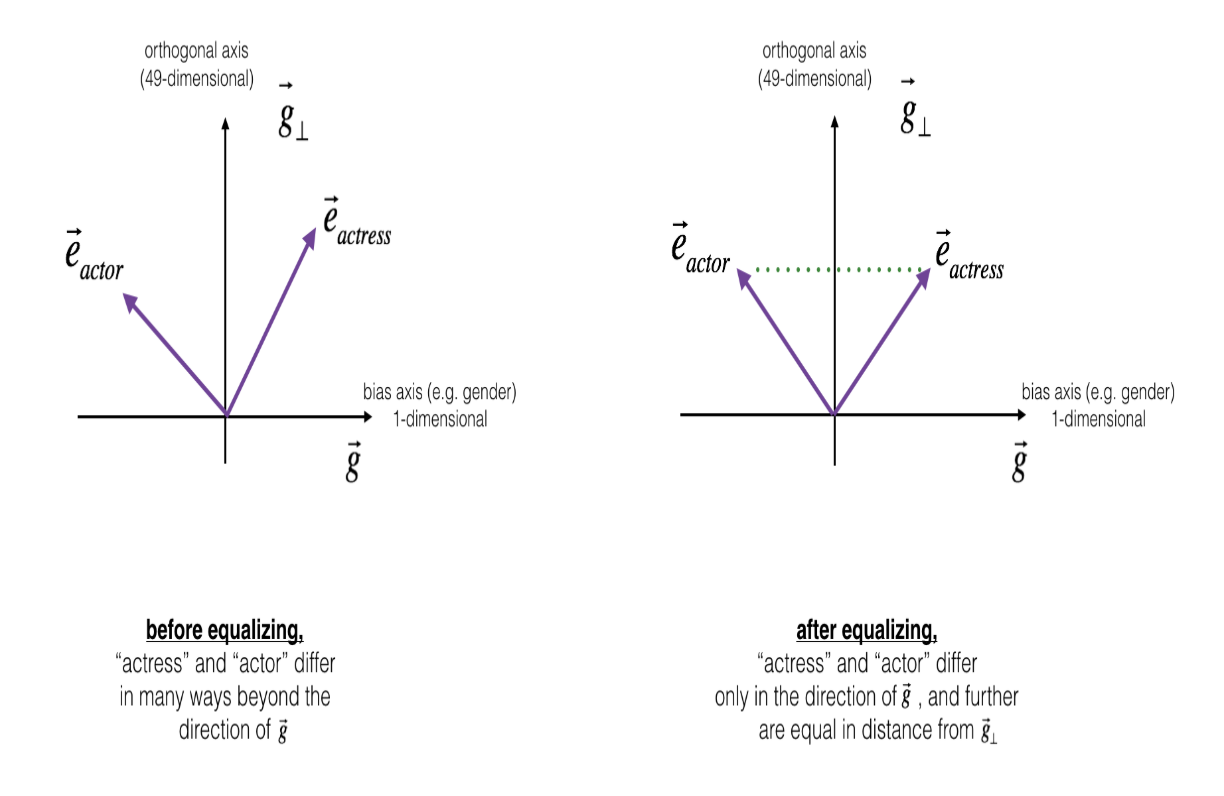
(2) Equalization algorithm for gender-specific words
- actress/actor 같은 경우 동일한 값을 가지도록 만들어주어야 함.
- 예를 들어 'babysit'의 경우, actor보다 actress와의 거리가 더 가깝다. 이런 경우에도 차이가 나지 않도록 만들어 주어야 함.

def equalize(pair, bias_axis, word_to_vec_map):
"""
Debias gender specific words by following the equalize method described in the figure above.
Arguments:
pair -- pair of strings of gender specific words to debias, e.g. ("actress", "actor")
bias_axis -- numpy-array of shape (50,), vector corresponding to the bias axis, e.g. gender
word_to_vec_map -- dictionary mapping words to their corresponding vectors
Returns
e_1 -- word vector corresponding to the first word
e_2 -- word vector corresponding to the second word
"""
### START CODE HERE ###
# Step 1: Select word vector representation of "word". Use word_to_vec_map. (≈ 2 lines)
w1, w2 = pair
e_w1, e_w2 = word_to_vec_map[w1], word_to_vec_map[w2]
# Step 2: Compute the mean of e_w1 and e_w2 (≈ 1 line)
mu = (e_w1 + e_w2) / 2
# Step 3: Compute the projections of mu over the bias axis and the orthogonal axis (≈ 2 lines)
mu_B = np.dot(mu, bias_axis) / (np.linalg.norm(bias_axis)**2) * bias_axis
mu_orth = mu - mu_B
# Step 4: Use equations (7) and (8) to compute e_w1B and e_w2B (≈2 lines)
e_w1B = np.dot(e_w1, bias_axis) / (np.linalg.norm(bias_axis)**2) * bias_axis
e_w2B = np.dot(e_w2, bias_axis) / np.sum(np.square(bias_axis)) * bias_axis
# Step 5: Adjust the Bias part of e_w1B and e_w2B using the formulas (9) and (10) given above (≈2 lines)
corrected_e_w1B = np.sqrt((1-(np.linalg.norm(mu_orth)))**2) * (e_w1B - mu_B) / (np.abs((e_w1 - mu_orth) - mu_B))
corrected_e_w2B = np.sqrt((1-(np.linalg.norm(mu_orth)))**2) * (e_w2B - mu_B) / (np.abs((e_w2 - mu_orth) - mu_B))
# Step 6: Debias by equalizing e1 and e2 to the sum of their corrected projections (≈2 lines)
e1 = corrected_e_w1B + mu_orth
e2 = corrected_e_w2B + mu_orth
### END CODE HERE ###
return e1, e2cosine similarities before equalizing:
cosine_similarity(word_to_vec_map["man"], gender) = -0.117110957653
cosine_similarity(word_to_vec_map["woman"], gender) = 0.356666188463
cosine similarities after equalizing:
cosine_similarity(e1, gender) = -0.710920529702
cosine_similarity(e2, gender) = 0.738567730352